人生亦有命,安能行叹复坐愁? —— 拟行路难·其四
目前只做字节跳动、腾讯的算法和后端的高频leetcode算法题。刷题之前先复习经典的一些算法,有相当多算法是经典算法的修改版。
汇总地址:
高频leetcode题🔥
数据结构与算法🔥
符号定义及含义
当输入规模足够大,使得运行时间只与增长量级有关时,需要研究算法的渐近效率。也就是,当输入规模无限增加时,在极限中,算法的运行时间如何随着输入规模的变大而增加。这里仅引入两个常用的渐进记号。
- $\Theta$ (西塔) 渐近紧确界,如$\frac{1}{2} n^{2}-3 n=\Theta\left(n^{2}\right)$,$6n^{3} \neq \Theta (n^{2})$,$n \neq \Theta (n^{2})$。
- $O$(大o)渐进上界,如 $\frac{1}{2} n^{2}-3 n=O\left(n^{2}\right)$,$6n^{3} \neq O(n^{2})$,$n = O (n^{2})$。
- 渐进记号代表的是集合,这里的$=$更多地代表$\in$。
- 算法复杂度分为时间复杂度和空间复杂度。时间复杂度衡量了执行算法所需要的计算工作量;而空间复杂度是指执行这个算法所需要的内存空间。
- 在相当多文献资料中,有时我们发现$O$记号非形式化地描述渐进确界,即已经使用$\Theta$记号定义的东西。
经典算法
经典排序算法
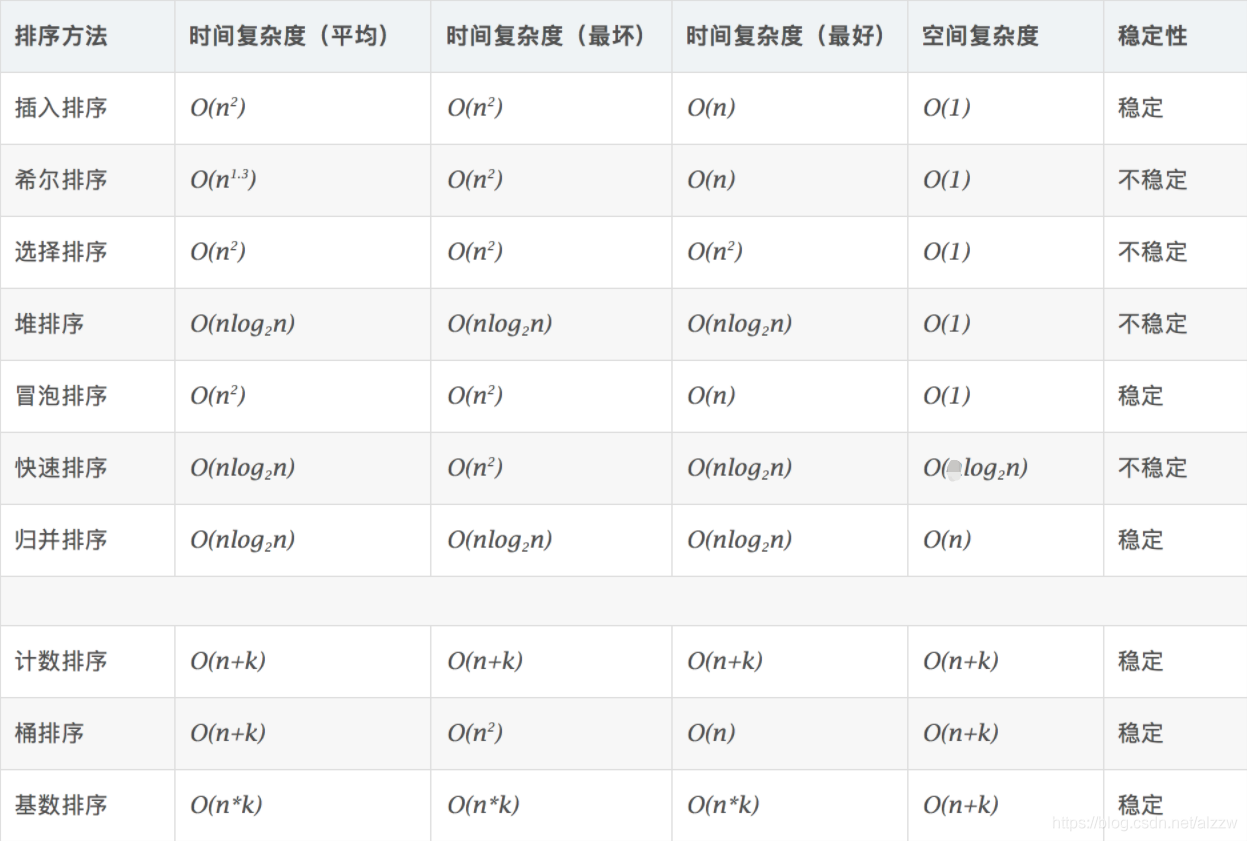
快速排序
python语言版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| def Quick_Sort(L, start, end):
if start < end:
i, j = start, end
base = L[i]
while i < j:
while(i < j) and (L[j] >= base):
j -= 1
L[i] = L[j]
while(i < j) and (L[i] <= base):
i += 1
L[j] = L[i]
L[i] = base
Quick_Sort(L, start, i - 1)
Quick_Sort(L, j + 1, end)
return L
|
C++ 语言版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| #include <iostream>
#include <vector>
#include <cassert>
using namespace std;
void quick_sort(vector<int> &v, int start, int end) {
if (start < end) {
int i = start;
int j = end;
int base = v[i];
while (i < j) {
while (i < j && v[j] >= base) j--;
v[i] = v[j];
while (i < j && v[i] <= base) i++;
v[j] = v[i];
}
assert(i == j);
v[i] = base;
quick_sort(v, start, i - 1);
quick_sort(v, i + 1, end);
}
}
|
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。如,输入: [3,2,1,5,6,4] 和 k = 2,输出: 5
python代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution:
def findKthLargest(self, nums: List[int], k: int) -> int:
if len(nums) == 1:
return nums[0]
left = 0
right = len(nums) - 1
# 还是默认从小到大排列吧
while left <= right: # 必须要等号!!
base = nums[left]
i = left
j = right
while i < j:
while i < j and nums[j] >= base:
j -= 1
nums[i] = nums[j]
while i < j and nums[i] <= base:
i += 1
nums[j] = nums[i]
nums[i] = base
if k == len(nums) - i:
return nums[i]
elif k > len(nums) - i:
# k = k - (len(nums) - i) 不要这行! 不用改变k
right = i - 1
else:
# k不变
left = i + 1
|
参考:快速排序-Python 实现
归并排序
python 语言版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| def mergesort(L):
"""归并排序"""
if len(L) <= 1:
return L
mid = len(L) // 2 # 将列表分成更小的两个列表
# 分别对左右两个列表进行处理,分别返回两个排序好的列表
left_L = mergesort(L[:mid])
right_L = mergesort(L[mid:])
# 对排序好的两个列表合并,产生一个新的排序好的列表
return merge(left_L, right_L)
def merge(left_L, right_L):
"""合并两个已排序好的列表,产生一个新的已排序好的列表"""
result = [] # 新的已排序好的列表
i = 0 # 下标
j = 0
# 对两个列表中的元素 两两对比。
# 将最小的元素,放到result中,并对当前列表下标加1
while i < len(left_L) and j < len(right_L):
if left_L[i] <= right_L[j]:
result.append(left_L[i])
i += 1
else:
result.append(right_L[j])
j += 1
result += left_L[i:]
result += right_L[j:]
return result
|
C++ 语言版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| #include <iostream>
#include <vector>
using namespace std;
void merge(vector<int>::iterator begin, vector<int>::iterator mid, vector<int>::iterator end, vector<int> &tmp_array) {
int idx = 0;
auto l = begin, m = mid, r = end;
while (l < mid && m < end) {
if (*l < *m) {
tmp_array[idx++] = *l;
++l;
} else {
tmp_array[idx++] = *m;
++m;
}
}
while (l < mid) {
tmp_array[idx++] = *l;
++l;
}
while (m < end) {
tmp_array[idx++] = *m;
++m;
}
// 拷贝
// assert()
for (int i = 0; i < idx; ++i) {
*(begin + i) = tmp_array[i];
}
}
void do_merge_sort(vector<int>::iterator begin, vector<int>::iterator end, vector<int> &tmp_array) {
int length = end - begin;
if (length <= 1) return;
auto mid = begin + length / 2;
do_merge_sort(begin, mid, tmp_array);
do_merge_sort(mid, end, tmp_array);
merge(begin, mid, end, tmp_array);
}
void merge_sort(vector<int> &array) {
vector<int> tmp_array(array.size(), 0);
do_merge_sort(array.begin(), array.end(), tmp_array);
return;
}
|
例题1:合并两个有序数组 (力扣88)
python代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution:
def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
"""
Do not return anything, modify nums1 in-place instead.
"""
# 将nums1后移n个位置
for i in range(m - 1, -1, -1):
nums1[i + n] = nums1[i]
idx = 0
p = n
q = 0
while p < m + n and q < n:
if nums1[p] < nums2[q]:
nums1[idx] = nums1[p]
idx += 1
p += 1
else:
nums1[idx] = nums2[q]
idx += 1
q += 1
while p < m + n:
nums1[idx] = nums1[p]
idx += 1
p += 1
while q < n:
nums1[idx] = nums2[q]
idx += 1
q += 1
return
|
数组
二分查找
例题1:爱吃香蕉的珂珂(力扣875)
珂珂喜欢吃香蕉。这里有 N 堆香蕉,第 i 堆中有 piles[i] 根香蕉。警卫已经离开了,将在 H 小时后回来。
珂珂可以决定她吃香蕉的速度 K(单位:根/小时)。每个小时,她将会选择一堆香蕉,从中吃掉 K 根。如果这堆香蕉少于 K 根,她将吃掉这堆的所有香蕉,然后这一小时内不会再吃更多的香蕉。
珂珂喜欢慢慢吃,但仍然想在警卫回来前吃掉所有的香蕉。
返回她可以在 H 小时内吃掉所有香蕉的最小速度 K(K 为整数)
分析
此题规约为在数组中寻找一个分解线,左右边符合不同的条件。
python代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution:
def minEatingSpeed(self, piles: List[int], h: int) -> int:
k_left = 1
k_right = max(piles)
while k_left < k_right:
mid = (k_left + k_right) // 2
if self.canFinish(piles, h, mid):
k_right = mid
else:
k_left = mid + 1 # 必须加1
return k_left
def canFinish(self, piles: List[int], h: int, k: int):
h_ = 0
for pile in piles:
h_ += pile // k
h_ += 1 if pile % k != 0 else 0
return h >= h_
|
例题2: x 的平方根 (力扣69)
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
python代码
1
2
3
4
5
6
7
8
9
10
11
| class Solution:
def mySqrt(self, x: int) -> int:
l, r, ans = 0, x, -1
while l <= r:
mid = (l + r) // 2
if mid * mid <= x:
ans = mid
l = mid + 1
else:
r = mid - 1
return ans
|
链表
链表翻转
python代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| class Solution:
def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:
if k == 1:
return head
# 多指针法
h = None
p = head
q = head
q_pre = None
n = 0
pre_last = None
while q != None:
q_pre = q
q = q.next
n += 1
if n == k:
n = 0
first, last = self.reverse(p, q_pre)
if h == None:
h = first
pre_last = last
else:
pre_last.next = first
pre_last = last
if n == 0:
pre_last.next = q
p = q
return h
# 翻转p节点和q节点之间的链表
def reverse(self, p: Optional[ListNode], q: Optional[ListNode]):
first = q
last = p
r = p.next
last.next = None
pre_r = None
q_next = q.next
while r != q_next:
pre_r = r
r = r.next
pre_r.next = p
p = pre_r
return first, last
|
二叉树
二叉树深度优先遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| # class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
# 先序遍历 Accepted
def preOrder(self, root: TreeNode) -> List[int]:
stack = [root]
res = []
while stack:
node = stack.pop()
if node:
res.append(node.val) # 访问
stack.append(node.right) # 先将右节点加入栈中
stack.append(node.left)
return res
# 中序遍历 Accepted
def inOrder(self, root: TreeNode) -> List[int]:
stack = []
res = []
while root or stack:
while root:
stack.append(root)
root = root.left
node = stack.pop()
res.append(node.val) # 访问
root = node.right
return res
# 后序遍历 Accepted
def postOrder(self, root: TreeNode) -> List[int]:
stack = []
res = []
preNode = None
while root or stack:
while root:
stack.append(root)
root = root.left
root = stack.pop()
if root.right == None or preNode == root.right: # 关键,取出来看看右边节点存在或者是否上次遍历过
res.append(root.val)
preNode = root
root = None # 避免重复访问左子树,不能丢
else:
stack.append(root)
root = root.right
return res
|
例题1:求根节点到叶节点数字之和(力扣129)
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
python代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| # class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.sum = 0
def sumNumbers(self, root: TreeNode) -> int:
self.sum = 0
self.do_sumNumbers(root, 0)
return self.sum
def do_sumNumbers(self, root: TreeNode, current: int):
if root == None: return
if root.left == None and root.right == None:
self.sum += current * 10 + root.val
else:
self.do_sumNumbers(root.left, current * 10 + root.val)
self.do_sumNumbers(root.right, current * 10 + root.val)
|
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。
python代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| # 完全按照自己的想法平铺直叙
class Solution:
def __init__(self):
self.res = None
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
self.res = None
self.dfs(root, p, q)
return self.res
def dfs(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> bool:
if root is not None:
left = self.dfs(root.left, p, q)
right = self.dfs(root.right, p, q)
node = True if root == p or root == q else False
if (left is True and right is True) or \
(left is True and node is True) or \
(right is True and node is True):
self.res = root
return True # return什么都可
elif (left is True) or (right is True) or (node is True):
return True
else:
return False
else:
return False
|
二叉树广度优先遍历(按层遍历)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| # class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
import queue
q = queue.Queue()
res = []
if root:
q.put(root)
next_level_size = 0 # 维护下次层节点的个数
cur_level_size = 1
level = []
while not q.empty():
node = q.get()
level.append(node.val)
cur_level_size -= 1
# None节点不入队列
if node.left:
q.put(node.left)
next_level_size += 1
if node.right:
q.put(node.right)
next_level_size += 1
if cur_level_size == 0:
res.append(level)
level = [] # 不能丢
cur_level_size = next_level_size
next_level_size = 0
return res
|
前序和中序遍历构造二叉树
python代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
length = len(preorder)
if not length:
return None
root = TreeNode(preorder[0])
i = inorder.index(preorder[0])
if i:
root.left = self.buildTree(preorder[1:1+i], inorder[0:i])
if length - i - 1: # 理解为右子树的节点数量
root.right = self.buildTree(preorder[1+i:length], inorder[i+1:])
return root
|
例题1:前序和中序遍历构造二叉树 (力扣98)
例题2:二叉树的右侧视图 (力扣199)
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
python代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution:
def solve(self , xianxu: List[int], zhongxu: List[int]) -> List[int]:
# write code here
# 10:21
# 引入深度变量
def build(preOrder: List[int], inOrder: List[int], depth: int):
length = len(preOrder)
if not length:
return
if len(res) > depth:
res[depth] = preOrder[0]
else:
res.append(preOrder[0])
i = inOrder.index(preOrder[0])
if i:
build(preOrder[1:i+1], inOrder[0:i], depth + 1)
if length - i - 1:
build(preOrder[i+1:], inOrder[i+1:], depth + 1)
res = []
build(xianxu, zhongxu, 0)
return res
|
二叉搜索树中序遍历
例题1:二叉搜索树中第K小的元素(力扣230)
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)。
python代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution:
def __init__(self):
self.n = 0
self.r = None
def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
self.n = 0
self.pre_visit(root, k)
return self.r
def pre_visit(self, root: Optional[TreeNode], k: int):
if root != None:
self.pre_visit(root.left, k)
self.n += 1
if self.n == k:
self.r = root.val
return
self.pre_visit(root.right, k)
|
python代码(官方)
1
2
3
4
5
6
7
8
9
10
11
12
| class Solution:
def kthSmallest(self, root: TreeNode, k: int) -> int:
stack = []
while root or stack:
while root:
stack.append(root)
root = root.left
root = stack.pop()
k -= 1
if k == 0:
return root.val
root = root.right
|
图结构
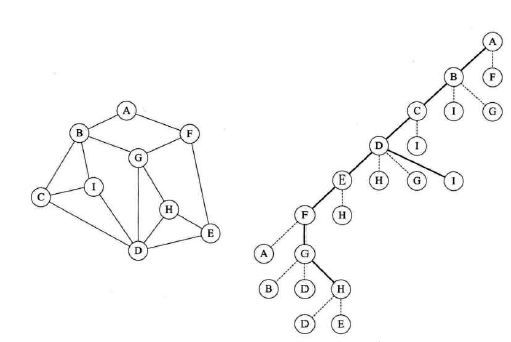
1
2
3
4
5
6
7
8
| G = [[0, 1, 1, 1, 1, 1, 0, 0],
[0, 0, 1, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 1, 0, 0, 0, 1, 1],
[0, 0, 0, 0, 0, 1, 0, 1],
[0, 0, 0, 0, 0, 1, 1, 0]]
|
图遍历
下面的代码都是github copilot自动生成的代码,看起来非常不错。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| # 假设图为无向连通图
# 图深度优先遍历
def dfs(G: List[List[int]], v: int) -> List[int]:
visited = [False] * len(G)
stack = [v]
res = []
while stack:
v = stack.pop()
if not visited[v]:
visited[v] = True
res.append(v)
for i in range(len(G)):
if G[v][i] == 1 and not visited[i]:
stack.append(i)
return res
# 图广度优先遍历
def bfs(G: List[List[int]], v: int) -> List[int]:
visited = [False] * len(G)
queue = [v]
res = []
while queue:
v = queue.pop(0)
if not visited[v]:
visited[v] = True
res.append(v)
for i in range(len(G)):
if G[v][i] == 1 and not visited[i]:
queue.append(i)
return res
# 图递归深度优先遍历
def dfs_recur(G: List[List[int]], v: int) -> List[int]:
visited = [False] * len(G)
res = []
def dfs_recur_helper(v: int):
if not visited[v]:
visited[v] = True
res.append(v)
for i in range(len(G)):
if G[v][i] == 1 and not visited[i]:
dfs_recur_helper(i)
dfs_recur_helper(v)
return res
# 图递归广度优先遍历
def bfs_recur(G: List[List[int]], v: int) -> List[int]:
visited = [False] * len(G)
res = []
def bfs_recur_helper(v: int):
if not visited[v]:
visited[v] = True
res.append(v)
for i in range(len(G)):
if G[v][i] == 1 and not visited[i]:
bfs_recur_helper(i)
bfs_recur_helper(v)
return res
|
参考:
图的两种遍历方式:DFS、BFS
给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
python代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
def dfs(i: int, j: int):
if i >= 0 and i < len(grid) and j >= 0 and j < len(grid[i]) and grid[i][j] == '1':
grid[i][j] = '0'
dfs(i - 1, j)
dfs(i + 1, j)
dfs(i, j - 1)
dfs(i, j + 1)
res = 0
for i in range(len(grid)):
for j in range(len(grid[i])):
if grid[i][j] == '1':
res += 1
dfs(i, j)
return res
|
其他例题
并查集
位运算
参考:位操作基础篇之位操作全面总结
动态规划算法
引子:计算斐波那契数列
斐波那契数列是指这样一个数列:0、1、1、2、3、5、8、13、21、34、55……
斐波纳契数列可以用下面的方法定义:
$$
\left\{
\begin{array}{l}
F(0) = 0, \\
F(1) = 1, \\
F(n) = F(n-1) + F(n-2), \quad n \geq 2 \text{ 为整数}
\end{array}
\right.
$$
如果我们要计算F(5),递归计算图如下:
 可以看到因为重复求解相同的子问题,使得浪费大量的计算时间和计算资源。那么求解斐波那契数列可以采用1)带有备忘录的递归算法;2)自底向上法。
可以看到因为重复求解相同的子问题,使得浪费大量的计算时间和计算资源。那么求解斐波那契数列可以采用1)带有备忘录的递归算法;2)自底向上法。
从斐波那契数列到动态规划
朴素递归算法之所以效率很低,是因为它反复求解相同的子问题。因此,动态规划方法仔细安排求解顺序,对每个子问题只求解一次,并将结果保存下来。如果随后再次需要此子问题的解,只需查找保存的结果,而不必重新计算。因此,动态规划方法时付出额外的内存空间来节省时间,是典型的时空权衡的例子。而时间上的节省可能是非常巨大的:可能将一个指数时间的解转化为一个多项式时间的解。
动态规划有两种等价的实现方法:
第一种方法称为带备忘的自顶向下。此方法仍按自然的递归形式编写过程,但过程或保存每个子问题的解(通常在一个数组或散列表)。当需要一个子问题的解时,过程首先检查是否已经保存过此解。如果是,则直接返回保存的值,从而节省了计算时间;否则,按通常方式计算这个子问题。称这个递归过程时带备忘的。
第二种方法称为自底向上法。这种方法一般需要恰当定义子问题“规模”的概念,使得任何子问题的求解都只依赖与“更小的”子问题的求解。因此可以将子问题按规模排序,按由小到大顺序进行求解。当求解某个子问题时,它所依赖的那些更小的子问题都已求解完毕,结果已经保存。每个子问题只需求解一次,当我们求解它时,它的所有前提子问题都已求解完成。
两种算法得到的算法具有相同的渐近运行时间,仅有的差异在某些特殊情况下,自顶向下方法并未真正递归地考察所有可能的子问题。由于没有频繁的递归函数调用的开销,自底向上方法的时间复杂性函数通常具有更小的系数。
动态规划题一般情况,需要先找到合适的状态转移方程/递推公式,中间结果状态的保存一般用数组或者多维数组,这里,如果状态转移方程只依赖之前计算的有限项,且这些有限项符合固定的规则,并且最后计算的结果不是在所有状态中寻找(如max)求得,那么往往并不需要一个数组,只需要记录某几个之前的状态(变量可以重复利用),就可以递推后面的情况,降低空间复杂度。该想法总结自求解斐波那契数列。
例题
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。如,输入:[2,7,9,3,1]
输出:12
递推公式
$$
\left\{\begin{array}{l}
dp[i][0] \text { 代表偷了第间房获得的最大收益 } \\
dp[i][1] \text { 代表没有偷第 } \mathrm{i} \text { 间房获得的最大收益 }
\end{array}\right.
$$
$$
\left\{\begin{array}{l}
d p[i+1][0]=dp[i][1]+L[i+1] \\
d p[i+1][1]=\max (d p[i][0], d p[i][1])
\end{array}\right.
$$
python代码
1
2
3
4
5
6
7
8
9
10
11
| class Solution:
def rob(self, nums: List[int]) -> int:
length = len(nums)
import numpy as np
dp = np.zeros((length, 2))
dp[0][0] = nums[0] # 偷了第i家获得的最大收益
dp[0][1] = 0 # 没偷了第i家获得的最大收益
for i in range(length - 1):
dp[i + 1][0] = dp[i][1] + nums[i + 1]
dp[i + 1][1] = max(dp[i][0], dp[i][1])
return int(dp.max())
|
优化之后的递推公式
用 $d p[i]$ 表示前 $i$ 间房屋能偷窃到的最高总金额, 那么就有如下的状态转移方程:
$$
d p[i]=\max (d p[i-2]+n u m s[i], d p[i-1])
$$
边界条件为:
$$
\begin{cases}d p[0]=n u m s[0] & \text { 只有一间房屋, 则偷窄该房屋 } \\ d p[1]=\max (n u m s[0], n u m s[1]) & \text { 只有两间房屋, 选择其中金额较高的房屋进行偷窃 }\end{cases}
$$
最终的答案即为 $d p[n-1]$, 其中 $n$ 是数组的长度。
例题2:零钱兑换 (力扣322)
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。计算并返回可以凑成总金额所需的最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。 如,输入:coins = [1, 2, 5], amount = 11,输出:3
分析
首先,想要凑成总金额又想使得所需的硬币个数最少,那么在组合中尽可能得使用更大面额的硬币;如果最大面额的硬币小于所需凑成的总金额,那么可以尝试先用一定数量的最大面额硬币,那么形成一个子问题为: 使用除去最大面额的硬币来凑成新总金额所需最小的硬币个数,新总金额 = 总金额 - 最大面额硬币 * 最大面额硬币个数。
python代码
1
2
3
4
5
6
7
8
9
| class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
dp = [float('inf')] * (amount + 1)
dp[0] = 0
for coin in coins:
for x in range(coin, amount + 1):
dp[x] = min(dp[x], dp[x - coin] + 1)
return dp[amount] if dp[amount] != float('inf') else -1
|
例题3: 最长有效括号(力扣32)
给你一个只包含 ‘(’ 和 ‘)’ 的字符串,找出最长有效(格式正确且连续)括号子串的长度。如,输入:s = “)()())",输出:4,解释:最长有效括号子串是 “()()”
python代码
1
2
3
4
5
6
7
8
9
10
| class Solution:
def longestValidParentheses(self, s: str) -> int:
n = len(s)
if n==0:return 0
dp = [0]*n
for i in range(len(s)):
# i-dp[i-1]-1是与当前)对称的位置
if s[i]==')' and i-dp[i-1]-1>=0 and s[i-dp[i-1]-1]=='(':
dp[i]=dp[i-1]+dp[i-dp[i-1]-2]+2 # 会出现dp[-1],然而没影响
return max(dp)
|
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数。
你可以对一个单词进行如下三种操作:插入一个字符、删除一个字符、替换一个字符。如:
输入:word1 = “horse”, word2 = “ros”
输出:3
解释:
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ’e’)
官方给的思路如何保证是全局最小操作数呢?另外,处理dp边界时候,可以申请一个额外的空间i=0,j=0,即申请dp[0…n + 1][0…m + 1]空间,然后把第一行和第一列的值设置为边界,这样递推代码中不用额外考虑边界情况,这样可以简化代码。
python代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution:
def minDistance(self, word1: str, word2: str) -> int:
if len(word1) == 0:
return len(word2)
if len(word2) == 0:
return len(word1)
# 递推式已经确定了,边界条件注意弄对就ok了!
# 这里其实可以申请n + 1, m + 1大小的二维数组
import numpy as np
n, m = len(word1), len(word2)
self.dp = np.zeros((n, m), dtype=int)
for i in range(n):
for j in range(m):
if word1[i] == word2[j]:
self.dp[i][j] = self.getDp(i - 1, j - 1)
else:
self.dp[i][j] = min(self.getDp(i, j - 1),
self.getDp(i - 1, j),
self.getDp(i - 1, j - 1)) + 1
return int(self.dp[n - 1][m - 1])
def getDp(self, i : int, j: int):
if i < 0 and j < 0:
return 0
if i < 0:
return j + 1
if j < 0:
return i + 1
return self.dp[i][j]
|
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列
看着有些难度,实际上只要想到动态规划,并且以nums[i]处作为子序列的结尾,从小递推到给定的序列的长度,就可以解决问题了。
python代码
1
2
3
4
5
6
7
8
| class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
dp = [1] * len(nums)
for i in range(len(nums)):
for j in range(i):
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j] + 1) # 更精简
return max(dp)
|
其他例题
动态规划中常用思想
- 增量法:字符串/矩阵表示的结构中,往往可以考虑尾部增加一个字符所带来的影响/变化,从而考虑多个情况,建立递归公式。
- 在字符串表示的结构中,任何一个子串/子序列,都必须有一个结尾字符,往往可以考虑将以字符结尾的某个DP变量作为动态规划状态,从而考虑更长的字符串。
奇淫技巧(小题大做)
待解决
小强有两个序列 a 和 b ,这两个序列都是由相同的无重复数字集合组成的,现在小强想把 a 序列变成 b 序列,他只能进行以下的操作:
从序列a中选择第一个或者最后一个数字井把它插入 a 中的任意位置。
问小强至少需要几次操作可以将序列 a 变为序列 b 。
输入描述:
一行一个整数 n 表示序列的长度。接下来两行每行 n 个整数。第一行表示序列a,第二行表示序列b。1≤ n ≤ $10^5;$1≤ $a_i$, $b_i$ ≤ $10^9$。保证给出的序列符合题意。
内推
字节跳动内推链接:字节内推,有需要的同学自取。
未归档
配置校验数
小华在开发配置校验功能时,发现配置的打开和关闭总是两两结对,为了减少这个状态的存储空间,小华将这些配置的“开°,“关“状态转换为1和0 的数组从左向右依次填充,如:
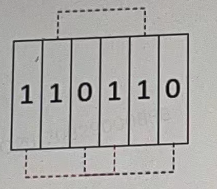
因为配置总是成对出现,所以数组长度为偶数,同时为了容易查找结对的配置,小华约定:对于 M 对配置,坐标 i 和 i+M 的配置组成一对。因为第一对配置必须开启,小华发现可以使用一个整数来表示,比如3,二进制表达为11,就代表一对配置同时打开,小华称之为配置校验数。
于是,小华突发其想,想研究一下这样能刚好表达结对配置同时打开或关闭的整數有多少个,现在请你设计一个程序,帮小华找出不大于给定的非负整数N的配置校验数有多少个。
基本计算器
[力扣224](https://leetcode.cn/problems/basic-calculator/)
c++ 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| # include <iostream>
# include <stack>
using namespace std;
class Solution {
public:
int calculate(string s) {
// 括号展开+栈
stack<int> ops;
ops.push(1);
int sign = 1;
int n = s.size();
int i = 0;
int ret = 0;
while (i < n) {
if (s[i] == ' ')
i++;
else if (s[i] == '+') {
sign = ops.top();
i++;
} else if (s[i] == '-') {
sign = -ops.top();
i++;
} else if (s[i] == '(') {
ops.push(sign);
i++;
} else if (s[i] == ')') {
ops.pop();
i++;
} else {
long num = 0;
for (; i < n && '0' <= s[i] && s[i] <= '9'; i++) {
num = 10 * num + s[i] - '0';
}
ret += sign * num;
}
}
return ret;
}
};
int main() {
Solution solution;
string s;
getline(cin, s);
cout << solution.calculate(s) << endl;
return 0;
}
|
参考:
动态规划课件和代码


 可以看到因为重复求解相同的子问题,使得浪费大量的计算时间和计算资源。那么求解斐波那契数列可以采用1)带有备忘录的递归算法;2)自底向上法。
可以看到因为重复求解相同的子问题,使得浪费大量的计算时间和计算资源。那么求解斐波那契数列可以采用1)带有备忘录的递归算法;2)自底向上法。