用矩阵推导网络。

符号定义

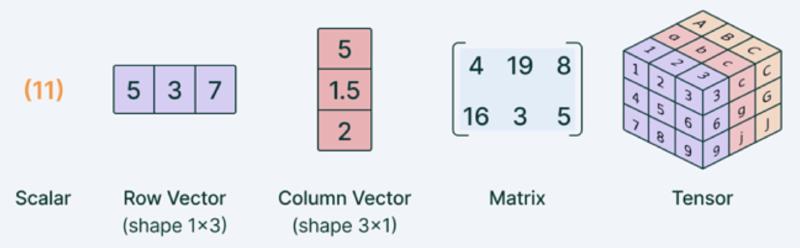
1. 使用小写字母$x$表示标量，粗体小写字母$\boldsymbol{x}$表示向量，注意向量可能为行向量或者列向量，大写字母$X$表示矩阵。
2. $\sigma$为逐元素sigmoid函数：$\sigma(z)=\frac{1}{1+\mathrm{e}^{-z}}$。
3. $\boldsymbol{1}$为列向量，$\boldsymbol{1}=(1, 1, 1 \cdots 1, 1, 1)^{T}$，非指示函数。
4. $exp(\boldsymbol{a})$表示逐元素求指数。
5. $log(\boldsymbol{a})$表示逐元素求自然对数。

符号含义

1. 列向量$\boldsymbol{x}=\left(x_{1}, x_{2}, x_{3} \cdots x_{n-2}, x_{n-1}, x_{n}\right)^{T}$代表一个输入样本，具有$n$个特征值。
2. 设列向量$\boldsymbol{z}=\left(z_{1}, z_{2}, z_{3} \cdots z_{n-2}, z_{n-1}, z_{n}\right)^{T}$，
   $\sigma(\boldsymbol{z}) = \left(\sigma(z_{1}), \sigma(z_{2}), \sigma(z_{3}) \cdots \sigma(z_{n-2}), \sigma(z_{n-1}), \sigma(z_{n})\right)$
3. 设列向量$\boldsymbol{a}=\left(a_{1}, a_{2}, a_{3} \cdots a_{n-2}, a_{n-1}, a_{n}\right)^{T}$，$\operatorname{softmax}(\boldsymbol{a})=\frac{\exp (\boldsymbol{a})}{\mathbf{1}^{T} \exp (\boldsymbol{a})}$，分母为行向量乘以列向量为标量，分子为列向量，所以结果仍为列向量。

运算法则

矩阵运算法则

1. 对尺寸相同的矩阵$A, B$，$\operatorname{tr}\left(A^{T} B\right)=\sum_{i, j} A_{i j} B_{i j}$。

矩阵微分运算符法则

1. 加减法、矩阵乘法、转置、求迹。

$$ d(X \pm Y)=d X \pm d Y $$ $$ d(X Y)=(d X) Y+X d Y $$ $$ d\left(X^{T}\right)=(d X)^{T} $$ $$ d \operatorname{tr}(X)=\operatorname{tr}(d X) $$

2. 求逆。

$$ d X^{-1}=-X^{-1} d X X^{-1} $$ 此式可以在 $ X X^{-1}=I $ 两侧求微分来证明。

3. 行列式。

$$ d|X|=\operatorname{tr}\left(X^{\ast} d X\right) $$

其中$X^{\ast}$表示$X$的伴随矩阵，在$X$可逆时，上式又可以写作为 $d|X|=|X|\operatorname{tr}\left(X^{-1} d X\right)$。此式可以用Laplace展开证明，详见张贤达《矩阵分析与应用》。

4. 逐元素乘法。

$$ d(X \odot Y)=d X \odot Y+X \odot d Y $$

$\odot$表示尺寸相同的矩阵$X$，$Y$逐元素相乘。

5. 逐元素函数。

$$ d \sigma(X)=\sigma^{\prime}(X) \odot d X $$

$\sigma(X)=\left[\sigma\left(X_{i j}\right)\right]$是逐元素标量函数运算，$\sigma^{\prime}(X)=\left[\sigma^{\prime}\left(X_{i j}\right)\right]$ 是逐元素求导数。例如： $$ X=\left[\begin{array}{ll} X_{11} & X_{12} \\ X_{21} & X_{22} \end{array}\right] $$

$$ d \sin (X)=\left[\begin{array}{ll} \cos X_{11} d X_{11} & \cos X_{12} d X_{12} \\ \cos X_{21} d X_{21} & \cos X_{22} d X_{22} \end{array}\right]=\cos (X) \odot d X $$

理解

1. 定义：标量f对矩阵 $X$ 的导数, 定义为 $\frac{\partial f}{\partial X}=\left[\frac{\partial f}{\partial X_{i j}}\right]$，即f对X逐元素求导排成与X尺寸相同的矩阵。

2. 将矩阵导数与微分建立联系：$d f=\sum_{i=1}^{m} \sum_{j=1}^{n} \frac{\partial f}{\partial X_{i j}} d X_{i j}=\operatorname{tr}\left(\frac{\partial f^{T}}{\partial X} d X\right)$。

3. 微分算子$d$作用于矩阵$X$，表示为逐元素作用。

4. 第一个等号是全微分公式，第二个等号表达了矩阵导数与微分的联系。

5. $tr()$代表迹(trace)是方阵对角线元素之和。

6. 举例：设$X=\left[\begin{array}{l}X_{0_0}, X_{01} \\ X_{10}, X_{11}\end{array}\right]$, $d X=\left[\begin{array}{l}dX_{00}, dX_{01} \\ dX_{10}, dX_{11}\end{array}\right]$，$\frac{d f}{d X}=\left[\begin{array}{ll}\frac{\partial f}{\partial X_{00}}, \frac{\partial f}{\partial X_{01}} \\ \frac{\partial f}{\partial X_{10}}, \frac{\partial f}{\partial X_{11}}\end{array}\right]$，$\operatorname{tr}\left(\frac{\partial f^{T}}{\partial X} d X\right)=\operatorname{tr}\left(\left[\begin{array}{ll}\frac{\partial f}{\partial X_{00}}, \frac{\partial f}{\partial X_{10}} \\ \frac{\partial f}{\partial X_{01}}, \frac{\partial f}{\partial X_{11}}\end{array}\right]\left[\begin{array}{l}dX_{00}, dX_{01} \\ dX_{10}, dX_{11}\end{array}\right]\right)$

思考

1. 样本特征值排列为列向量，方便统一形式为权重参数$W$放在$\boldsymbol{x}$前，进行乘积。

全连接网络

$$ l=-\boldsymbol{y}^{T} \log \operatorname{softmax}\left(W_{2} \sigma\left(W_{1} \boldsymbol{x}\right)\right) $$

符号说明

1. $l$为损失函数。
2. $\boldsymbol{x}$为单样本，则$l$只包含一个样本的损失函数。
3. 分类网络类别数为$m$，$\boldsymbol{y}$ 是除一个元素为1外其它元素为 0 的的 $m \times 1$ 列向量, $W_{2}$ 是 $m \times p$ 矩阵, $W_{1}$ 是 $p \times n$ 矩阵, $\boldsymbol{x}$ 是 $n \times 1$ 列向量, $l$ 是标量

推导 $\frac{\partial l}{\partial W_{1}}$ 和 $\frac{\partial l}{\partial W_{2}}$

定义：

$\boldsymbol{a_{1}}=W_{1}\boldsymbol{x}$

$\boldsymbol{h}_1=\sigma\left(\boldsymbol{a}_1\right)$

$ \boldsymbol{a_{2}}=W_{2}\boldsymbol{h_{1}}$ $l=-\boldsymbol{y}^{T} \log \operatorname{softmax}\left(\boldsymbol{a}_{2}\right)$

已知 $\frac{\partial l}{\partial \boldsymbol{a_{2}}}=\operatorname{softmax}\left(\boldsymbol{a}_{2}\right)-\boldsymbol{y}$ 。

推导结果： $$ \frac{\partial l}{\partial W_{2}}=\frac{\partial l}{\partial \boldsymbol{a_{2}}} \boldsymbol{h_{1}}^{T} $$ $$ \frac{\partial l}{\partial W_{1}}=\frac{\partial l}{\partial \boldsymbol{a}_{1}} \boldsymbol{x}^{T} $$

推广到多个样本

使用矩阵来表示N个样本，以简化形式。

定义：

$X=\left[\boldsymbol{x_{1}}, \cdots, \boldsymbol{x_{N}}\right]$

$A_{1}=\left[\boldsymbol{a_{1,1}}, \cdots \boldsymbol{a_{1, N}}\right]=W_{1} X+\boldsymbol{b_{1}} \mathbf{1}^{T}$

$H_{1}=\left[\boldsymbol{h_{1,1}}, \cdots, \boldsymbol{h_{1, N}}\right]=\sigma\left(A_{1}\right)$

$A_{2}=\left[\boldsymbol{a_{2,1}}, \cdots, \boldsymbol{a_{2, N}}\right]=W_{2} H_{1}+\boldsymbol{b_{2}} \mathbf{1}^{T}$

注意这里使用全$\mathbf{1}$向量来扩展维度。

推导结果：

$$ \frac{\partial l}{\partial W_{1}}=\frac{\partial l}{\partial A_{1}} X^{T}, \quad \frac{\partial l}{\partial \boldsymbol{b_1}}=\frac{\partial l}{\partial A_{1}} \mathbf{1} $$

$$ \frac{\partial l}{\partial W_{2}}=\frac{\partial l}{\partial A_{2}} H_{1}^{T}, \quad \frac{\partial l}{\partial \boldsymbol{b_2}}=\frac{\partial l}{\partial A_{2}} \mathbf{1} $$

参考

神经网络的一些公式总结
矩阵求导术（上）
矩阵求导术（下）

更新记录

调整格式和排版。 —— 2022.07.19

使用 pandoc 渲染，对公式展示更友好。 —— 2022.08.27