前言

人工神经网络（Artificial Neural Network，ANN）是一门重要的机器学习技术。它是目前最为火热的研究方向–深度学习（Deep Learning）的基础。学习神经网络不仅可以让你掌握一门强大的机器学习方法，同时也可以更好地帮助你理解深度学习技术。

四年前，韩国围棋九段棋手李世石与谷歌人工智能 AlphaGo 之间的围棋比赛，最终 AlphaGo 以四比一取胜，这让人工智能 AlphaGo 背后的技术——深度学习算法大火，笔者也是从这个时候开始关注深度学习，对计算机领域产生了兴趣。此后一年，谷歌又推出 AlphaGo 围棋升级版，并邀请世界围棋冠军、中国棋手柯洁于 2017 年 5 月份与之进行围棋大战，笔者全程直播观看了 AlphaGo 与柯洁人机围棋大战，在看到作为人类智慧的顶峰柯洁含泪认输后，笔者被 AlphaGo 背后的技术神经网络所深深震撼（还包括另一种技术：蒙特卡洛树搜索）。围棋不同于其他棋，计算机目前无法遍历围棋的所有可能的下法，所以算法必须尝试模拟人类大脑的下棋，根据以往学习到的经验判断落棋点，而不是暴力遍历所有可能性后选择最佳的下棋点，从而取胜。

这篇文章试图介绍深度学习中很重要的技术——神经网络，并重点介绍神经网络中运用到反向传播算法。

在笔者大学期间，除了两场围棋人机大战外，还有一场比较有意思的大型实验：大贝尔实验——关于验证基础物理量子力学中非常有名且重要的贝尔不等式的实验。所谓“遇事不决，量子力学”，这个梗就表示了量子力学中存在一些无法解释（宏观世界难以理解）的现象，若有兴趣可以再了解下。

感知机

感知机介绍

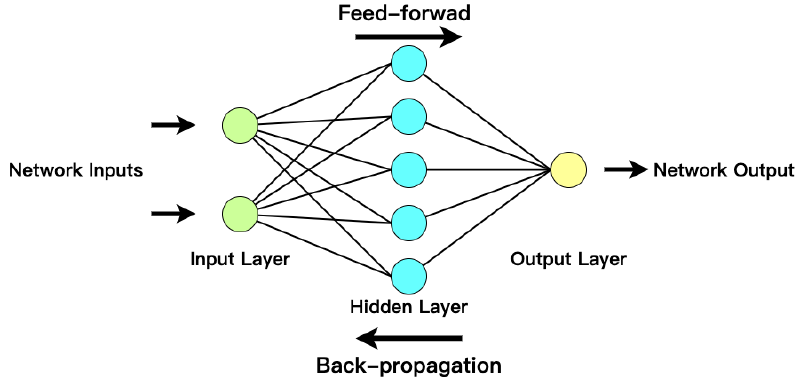
首先让我们先来了解下神经网络中最简单也是最基础的一种结构——感知机（Perceptron），如下图：

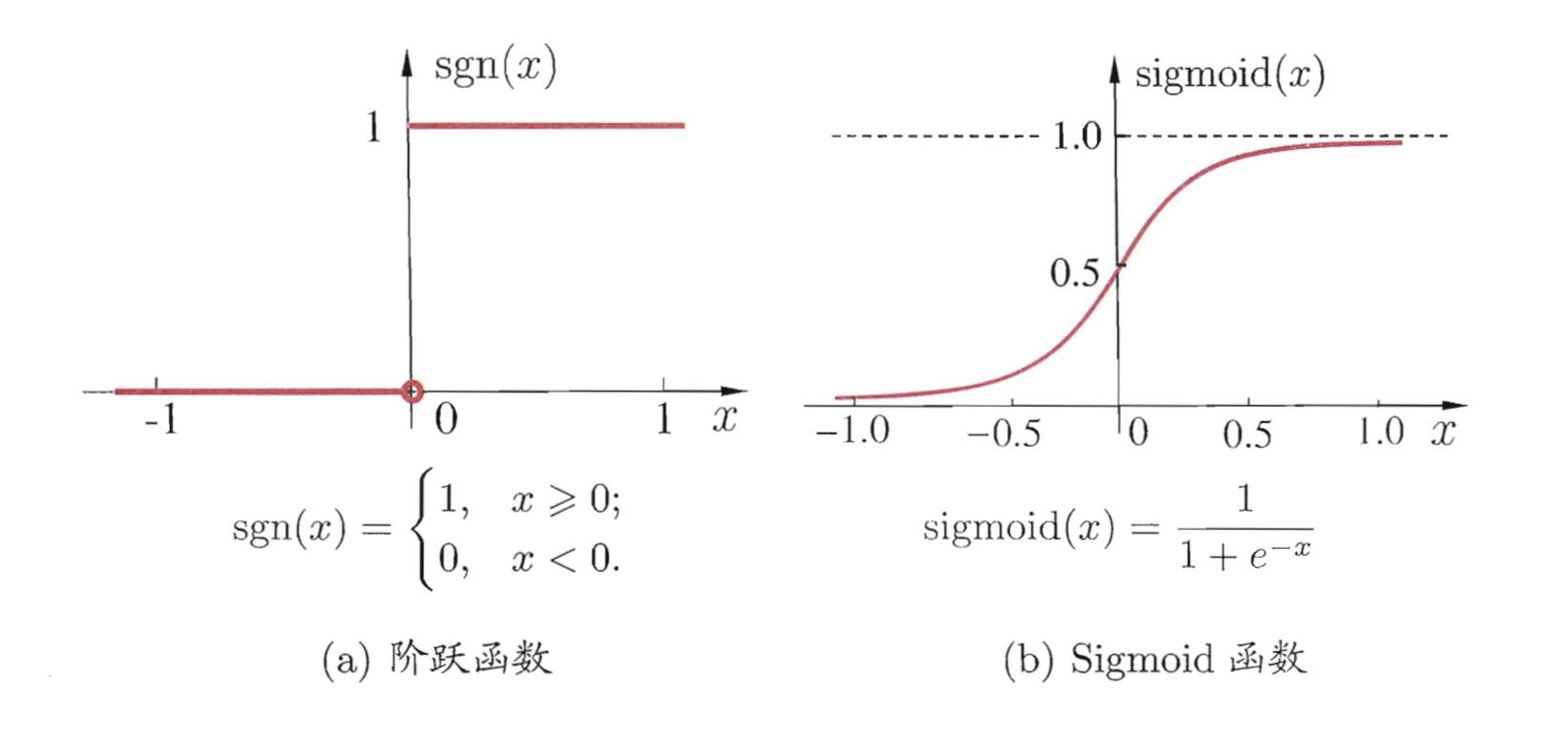
研究者模拟生物神经网络中的一个简单的神经元的行为——神经元兴奋过程，与之对应的感知机基础概念被提出，这里我们可以把权重当作突触、把偏置当作阈值以及把激活函数当作细胞体，当经过突触的信号总和超过了某个阈值（偏置项），细胞体就会兴奋（激活函数），产生电脉冲（输出 1），而当信号量总和未超过阈值，不产生电脉冲（输出 0）。它可以被视为一种最简单形式的前馈神经网络，是一种二元线性分类器。感知机（单个神经元）代表了从输入空间到输出空间的如下函数： $$ y = f(\sum_{i=1}^{n}w_ix_i + b) $$ 理想中的激活函数$f(·)$是下图 a 所示的阶跃函数，输出“1”对应神经元兴奋，输出“0”对应神经元抑制，然而阶跃函数具有不连续、不光滑等不太好的数学性质，因此实际常用 Sigmoid 函数作为激活函数，如下图 b 所示，该函数将实域范围的输出挤压到（0，1）范围输出，也被称为“挤压函数”。 对于感知机模型的理解：感知机模型的假设空间（容量）是定义在特征空间中的所有线性分类模型或线性分类器。感知机对应函数值为 0，即$w·x + b = 0$，对应于特征空间$R^n$中的一个超平面$S$，其中$w$是超平面的法向量，$b$是超平面的截距，这个超平面将特征空间划分为两个部分，位于两部分空间中的点分别被分为正、负两类。

感知机学习策略

感知机学习以最小化误分类点到超平面$S$的总距离为目标，因此感知机学习算法是误分类驱动的，具体使用时采用随机梯度下降法。 误分类点到超平面的总距离为 $$ -\frac{1}{||w||}\sum_{x_i\in M}y_i(w·x_i + b) $$ 其中$(x_i, y_i)$为样本点，$M$为误分类点的集合，对于误分类点来说$-y_i(w·x_i + b) > 0$成立，且当$(w·x_i + b) > 0$时，$y_i = -1$，当$(w·x_i + b) < 0$时，$y_i = +1$。 不考虑$\frac{1}{||w||}$，就得到感知机学习的损失函数为 $$ L(w, b) = -\sum_{x_i\in M}y_i(w·x_i + b) $$ 损失函数的梯度为 $$ \nabla_w L(w, b) = - \sum_{x_i\in M}y_ix_i$$ $$ \nabla_b L(w, b) = - \sum_{x_i\in M}y_i$$

采用随机梯度下降法，随机选取一个误分类点$(x_i, y_i)$，对$w, b$进性更新： $$ w \leftarrow w + \eta y_ix_i $$ $$ b \leftarrow b + \eta y_i $$

具体推导过程及算法迭代过程参见李航《统计学习方法》，代码实现参见此 github。

感知机模型存在的问题

感知机的学习能力非常有限，与、或、非问题都是线性可分的，所以感知机可以处理，但是感知机却不能解决异或简单的非线性可分问题。 异或问题暴露出这样一个问题，即在现实任务中，原始样本空间内也许并不存在一个能正确划分两类样本的超平面，对于这样的问题，一种方法，1) 可将样本从原始空间映射到一个更高维的特征空间（或者不用更高维也可以），所谓的核函数$\phi$，使得样本在这个特征空间内线性可分，幸运的是，如果原始空间是有限维，那么一定存在一个高维特征空间使得样本线性可分。2) 另一种方法，通过增加感知机的层数，使得形成一个神经网络，其中输入层神经元接受外界输入，隐层与输出层神经元对信号进行加工，最终结果由输出层神经元输出。（花书理解：深层神经网络中的隐藏层即代表输入经过了一个核函数$\phi$变换，那么以上两种方式都是在寻找一个恰当的核函数$\phi$，神经网络的方式是通过网络自主学习学到恰当的核函数）

神经网络

神经网络介绍

考虑到感知机模型存在的问题，即只能解决线性可分问题，我们将感知机进行连接，形成多层感知机——神经网络，如下图

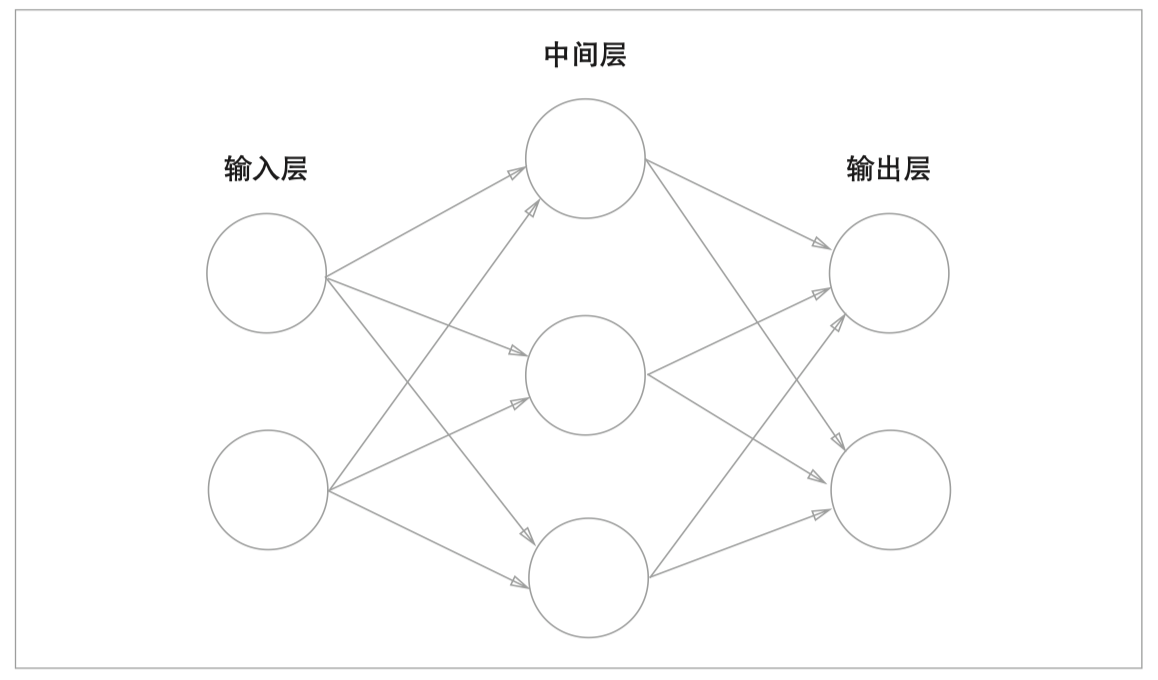
神经网络其实就是按照一定规则连接起来的多个神经元。上图展示了一个全连接(full connected, FC)神经网络，通过观察上面的图，我们可以发现它的规则包括：

• 神经元按照层来布局。最左边的层叫做输入层，负责接收输入数据；最右边的层叫输出层，我们可以从这层获取神经网络输出数据。输入层和输出层之间的层叫做隐藏层，因为它们对于外部来说是不可见的。
• 同一层的神经元之间没有连接。
• 第N层的每个神经元和第N-1层的所有神经元相连(这就是full connected的含义)，第N-1层神经元的输出就是第N层神经元的输入。
• 每个连接都有一个权值。

上面这些规则定义了全连接神经网络的结构。事实上还存在很多其它结构的神经网络，比如卷积神经网络(CNN)、循环神经网络(RNN)，他们都具有不同的连接规则。

用矩阵形式表示神经网络运算过程，如下： 第一层加权和为 $$ A^{(1)} = XW^{(1)} + B^{(1)} $$ 其中，$X$为$N\times2$大小矩阵，$N$代表输入神经网络的数据有$N$个样本，$2$代表每个样本有两个特征值；$W$为$2\times3$大小的矩阵代表输入层到中间层的线性变换权重矩阵；$B$为偏置项。 第一层激活后为 $$ Z^{(1)} = sigmoid(A^{(1)}) $$ 其中 sigmoid 函数作用于$A^{(1)}$中的每一个元素。将第一层的输出$Z^{(1)}$作为第二层的输入，同理得： $$ A^{(2)} = Z^{(1)}W^{(2)} + B^{(2)} $$ 注意： 因为单隐层神经网络只经过两层传播，那么第二层的输出就是网络的输出，这里一般（1）回归问题使用恒等函数作为激活函数，（2）分类问题可以使用 softmax 函数。我们把此神经网络看作是分类采用 softmax 函数： $$ y_k = \frac{exp(a_k)}{\sum_{i=1}^{n}exp(a_i)} $$ 那么神经网络的输出为 $$ Y = softmax(A^{(2)}) $$ 其中$Y$为$N\times2$矩阵，形如：

$$ \left[ \begin{array}{ccc} 0.2650877& 0.7349123\\ \vdots & \vdots\\ 0.8987211 & 0.1012788\\ \end{array} \right] $$

代表第一个样本预测为第二个分类概率为 0.7349123，大于 0.5，可以认为预测为第二个分类；最后一个样本预测为第一个分类概率为 0.8987211，可以认为预测为第一个分类。（当然只有两个样本的情况下一般看作正类和负类，只需要一个输出神经元，使用 sigmoid 函数激活即可。）该模型使用 softmax 函数作为激活函数，可以推广到多分类情况下。

神经网络学习策略

神经网络的学习中使用的指标为损失函数（loss function），即以最小化损失函数为目标，理论上，损失函数可以使用任意函数，但实际中一般用均方误差和交叉熵误差等。 均方误差为 $$ E = \frac{1}{2}\sum_{k}(y_k - t_k)^2 $$ 交叉熵误差为 $$ E = -\sum_{k}t_k\log_e{y_k} $$ 其中$y_k$表示神经网络的输出，$t_k$表示监督数据，k 表示数据的维度，如在手写数字识别例子中，$y_k$、$t_k$如下 10 个元素构成的数据：

1
2

y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]

在批量样本学习中，可以将对所有的样本的单个误差求和，然后再除以样本数 N，求得单个数据的“平均损失函数”，将它作为损失函数。 神经网络学习的策略和感知机学习策略都是一个最优化问题，神经网络学习中也是采用随机梯度下降法，与感知机学习策略更新参数类似，对于神经网络任意参数（线性权重、线性偏置等需要学习参数）更新估计式如下 $$ v \leftarrow v + \Delta v $$ 更新参数为线性连接权重参数时 $$ w_{hj} \leftarrow w_{hj} + \Delta w_{hj} $$ 采用梯度下降法，有 $$ w_{hj} \leftarrow w_{hj} - \eta \frac{\partial E}{\partial w_{hj}} $$ 对于梯度求解，一般有解析法和数值法两种方法，随着神经网络神经元增加和层数增加，直接求上万，甚至上亿个参数的解析导数变得不现实，计算量非常大。下面将介绍两种数值方式计算梯度方法：导数定义法和反向传播法。

梯度计算

梯度在直角坐标系下计算公式为 $$ \nabla f(x) = (\frac{\partial f(x)}{\partial x_1}, \frac{\partial f(x)}{\partial x_2}, …) $$ 梯度计算的结果是一个向量，并且可以看到计算梯度需要求函数对于各个自变量的偏导数。 对于多元函数，偏导表示自变量某个瞬间的变化量。定义为如下： $$ \frac{\partial f(x_1, x_2, x_3…x_i…)}{\partial x_i} = \lim_{h \to 0} \frac{f(x_1, x_2, x_3…x_i + h, …)}{h} $$ 偏导的定义和导数的定义类似，表示自变量上“微小的变化”将导致函数$f(x)$的值在多大程度上发生变化。我们可以直接用程序实现上面的计算方式，程序中无法表示 h 趋近 0，我们使用一个微小值代替，计算近似解。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

# 数值梯度
def numerical_gradient(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)  # 生成和x形状相同的数组

    for idx in range(x.size):
        tmp_val = x[idx]
        # 计算f(x+h)
        x[idx] = tmp_val + h
        fxh1 = f(x)

        # 计算f(x-h)
        x[idx] = tmp_val - h
        fxh2 = f(x)

        grad[idx] = (fxh1 - fxh2) / (2*h)
        x[idx] = tmp_val # 还原x的值

    return grad

上面程序实现的偏导数方式和上面公式稍有不同，使用中心差分，误差比前向差分小，学过微积分的同学应该能够明白。虽然上面求偏导数看着很方便很简单，但是根据上面的方式计算梯度在面对神经网络这种具有很大规模输入和很大规模参数时，计算效率相当慢。下面将重点介绍反向传播算法计算梯度。（介绍完反向传播算法后，还会再介绍两者求解方式差异，为什么上面方式求解梯度速度在神经网络应用上效率太慢）

计算图

为了更精确地描述反向传播算法，我们使用计算图（computational graph）语言来描述一系列操作。《深度学习》花书和斯坦福李飞飞 cs231n 课程对于计算图表示上有些区别，但都表示同一个含义，即用图的方式形式化地将操作次序表示出来，方便理解。这里我们介绍 cs231n 课程对于计算图的画法。 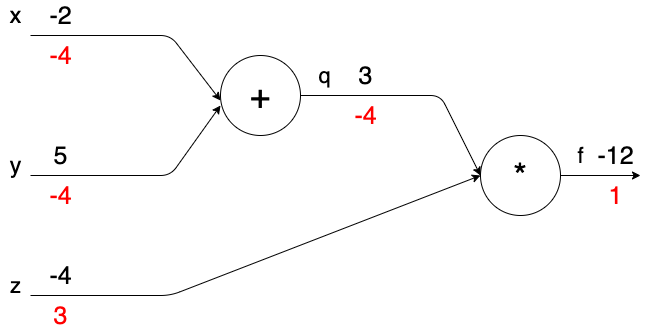使用圆圈代表操作节点，指向节点的箭头代表输入变量，从节点指出的箭头代表操作完后输出的变量。上面计算图即表示了$f(x,y,z) = (x + y)z$。

反向传播算法

简单标量反向传播算法

上面计算图真实值计算线路展示了计算的视觉化过程。前向传播从输入计算到输出（绿色），反向传播从尾部开始，根据链式法则递归地向前计算梯度（显示为红色），一直到网络的输入端。可以认为，梯度是从计算链路中回流。 如上图计算过程，可以用下面几个中间过程合成： $$ q = x + y $$ $$ f = q \times z $$ 在输入$x = -2, y = 5, z = -4$情况下，箭头下面红色数字代表 f 对该处变量的偏导，即 $$ \frac{\partial f}{\partial f} = 1 $$ $$ \frac{\partial f}{\partial q} = \frac{\partial (q \times z)}{\partial q} = z\vert_{z=-4}=-4 $$ $$ \frac{\partial f}{\partial z} = \frac{\partial (q \times z)}{\partial z} = q\vert_{q=3}=3 $$ 根据求导的链式法则得 $$ \frac{\partial f}{\partial x} = \frac{\partial f}{\partial q}\frac{\partial q}{\partial x}=1 \cdot (-4) \cdot 1 = -4 $$ $$ \frac{\partial f}{\partial y} = \frac{\partial f}{\partial q}\frac{\partial q}{\partial y}=1 \cdot (-4) \cdot 1 = -4 $$ 结合上面计算图和求导的链式法则可以有以下结论： “$输出结果对某一变量的偏导 = 反向传播时上游传递下来的偏导数 \times 本地偏导数（该变量输入的计算节点偏导数）$” 下面介绍稍微复杂的计算图，如下图。 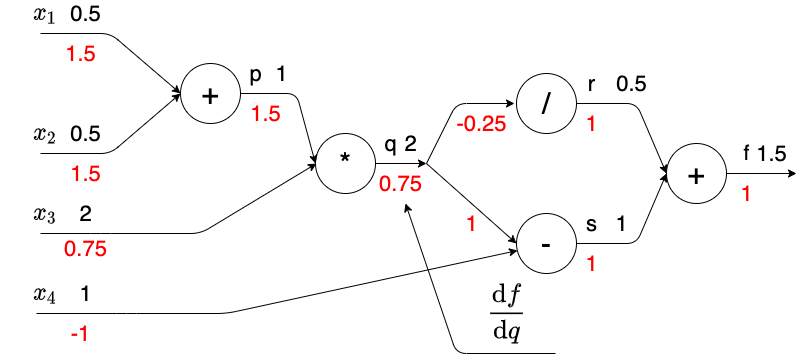利用上面得到的结论就可以得到每个遍历的偏导数，这个计算图和上面计算图区别之处在于：在乘法节点的结果输出到两个节点，分别是除法节点和减法节点，导数反向传播时，需要将上游传递的两个导数相加，即-0.25 + 1 = 0.75 这是基于下面的定理：

定理：若函数$u=\varphi(t), v=\psi(t)$在点 t 可导，$z=f(u,v)$在点(u,v)处偏导连续，则复合函数$z=f(\varphi(t),\psi(t))$在点 t 可导，则有链式法则 $$ \frac{\mathrm{d} z }{\mathrm{d} t} = \frac{\partial z}{\partial u} \cdot \frac{\mathrm{d} u }{\mathrm{d} t} + \frac{\partial z}{\partial v} \cdot \frac{\mathrm{d} v }{\mathrm{d} t} $$

矩阵形式反向传播算法

下面介绍矩阵形式计算图及反向传播公式，如下图神经网络 Affine 层。

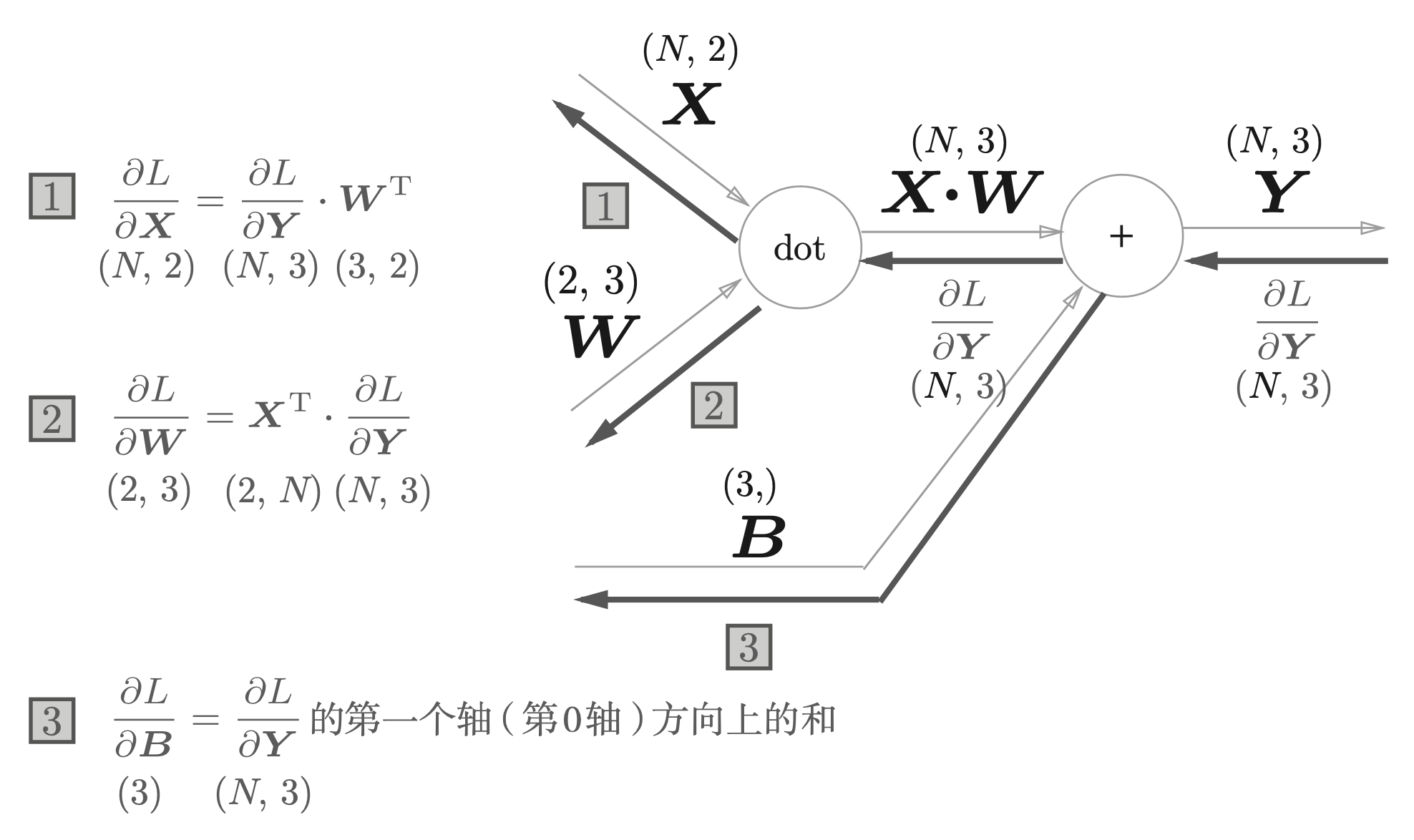
Affine 层：神经网络在正向传播中进行的矩阵的乘积运算在几何学领域被称为“仿射变换”。因此，这里将进行的仿射变换的处理称为“Affine 层”。

神经网络中还有其他比较复杂的层，梯度推导比上面 Affine 层线性偏导数推导更为复杂，在此略过介绍及推导，但运用到的知识与上面方式类似，强烈建议自己手动推导下 Affine 层反向传播，对自己理解有帮助。

前面介绍神经网络学习策略也是一个最优化问题，即 $$ loss \ function = E = \varphi(y, t) $$ 损失函数/目标函数为预测值$y$和监督数据$t$的函数，其中$y$是经过神经网络正向传播得到的预测值，所以$y$是神经网络所有参数$W$的函数，那么目标函数是关于参数$W$的函数（凸函数），即 $$ loss \ function = \psi(\textbf{W}) $$ 根据梯度下降法，需要求得 $$ \frac{\partial L}{\partial \textbf{W}} $$ 这里的$L$表示$loss function$，也即是$E$。根据上面的神经网络反向传播算法逐层传播梯度，即可以高效地求解损失函数对参数的梯度，再根据随机梯度下降法，不断更新权重参数$W$，最小化目标函数，完成简单神经网络的训练学习。

反向传播算法特别之处

现代的神经网络规模和层数不断增加，一个复杂的深度学习模型，可能每一层有成百量级神经元，有上百层深度，下图显示一个较复杂的神经网络。 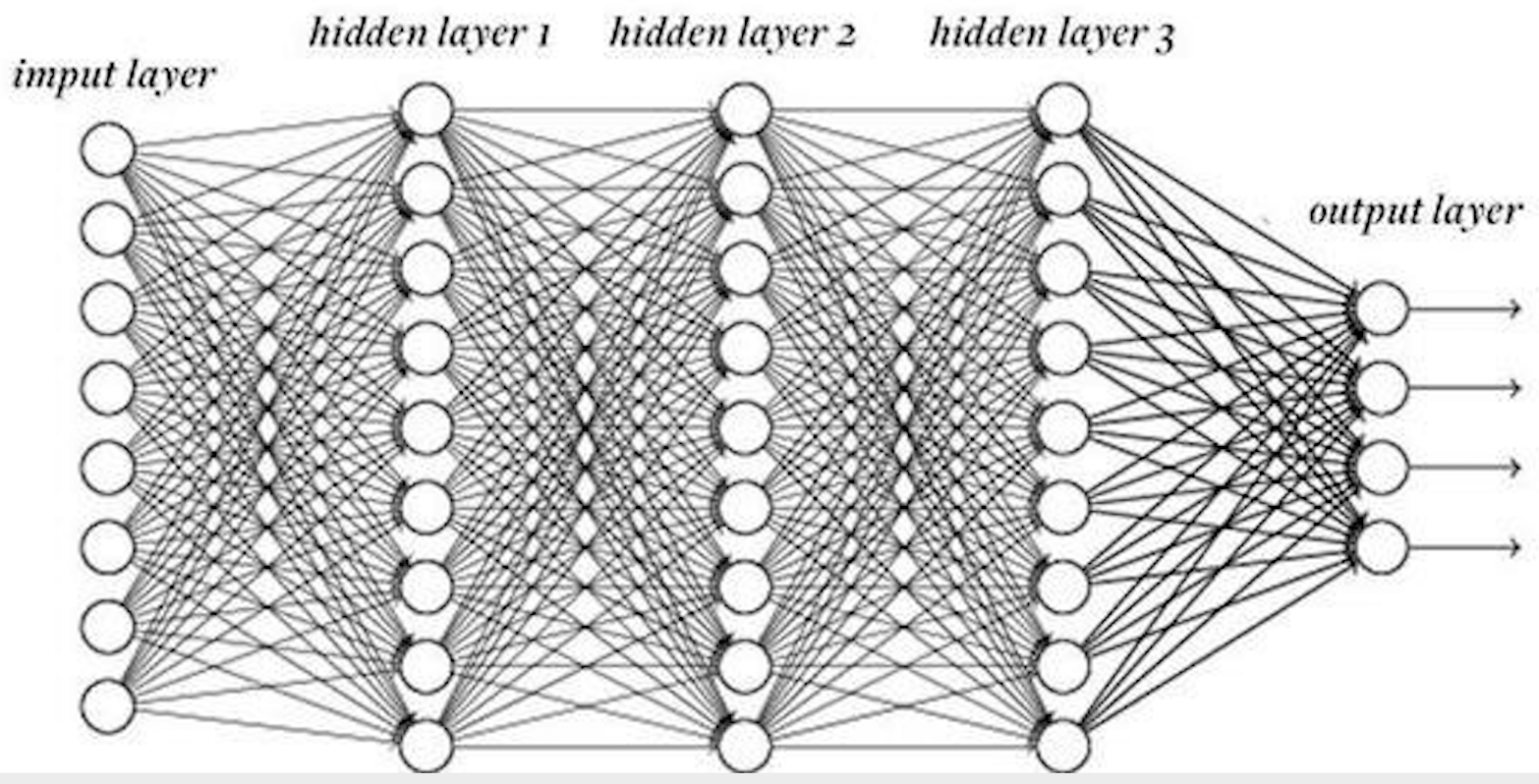如果采用导数定义方式，即$\frac{\partial L(w)}{\partial w} = \lim_{w \to 0} \frac{f(w + h)}{w}$求解，那么在求解每一个权重（即一条连接边）参数的偏导数时神经网络都需要向前传递一次，可以看到因为越靠后的神经元被重复计算的次数就越多，随着神经元个数和层数的增加，这将会是个指数增加的时间复杂度。然而，利用了函数求导的链式法则，从输出层到输入层逐层计算模型参数的梯度值，可以看到按照这个方向计算梯度，各个神经单元只计算了一次，没有重复计算。这个计算方向能够高效的根本原因是：在计算梯度时前面的单元是依赖后面的单元的计算，而“从后向前”的计算顺序正好“解耦”了这种依赖关系，先算后面的单元，并且记住后面单元的梯度值，计算前面单元的梯度时就可以充分利用已经计算出来的结果，避免了重复计算。

总结与思考

如今人工智能领域中最重要的算法——反向传播算法其主要思想本质也是利用了动态规划，这种方法结合了解析法计算梯度和数值法计算梯度，利用空间换取时间，缩短求解大量参数梯度的时间，从而加速神经网络的训练。反向传播算法看上去高大上，但也不见得是用了多高级的方法和高深的知识。

参考资料：
维基百度-感知器
维基百度-人工神经网络
计算机的潜意识
《Deep Learning form Scratch》
《深度学习》
周志华《机器学习》
《深度学习[花书]》
李航《统计学习方法》
零基础入门深度学习(3) - 神经网络和反向传播算法(牛逼)