卷积计算底层实现

为了更深入理解卷积神经网络，这篇博客介绍在卷积神经网络中常用的卷积操作底层是如何实现的。

卷积

卷积本身的执行过程是通过在特征图上滑动卷积核来完成的，如下面两个动图，形象地展示了单通道卷积和多通道卷积操作。

单通道卷积

多通道卷积

多通道卷积计算底层实现

假设输入图像及卷积和大小如下图所示：

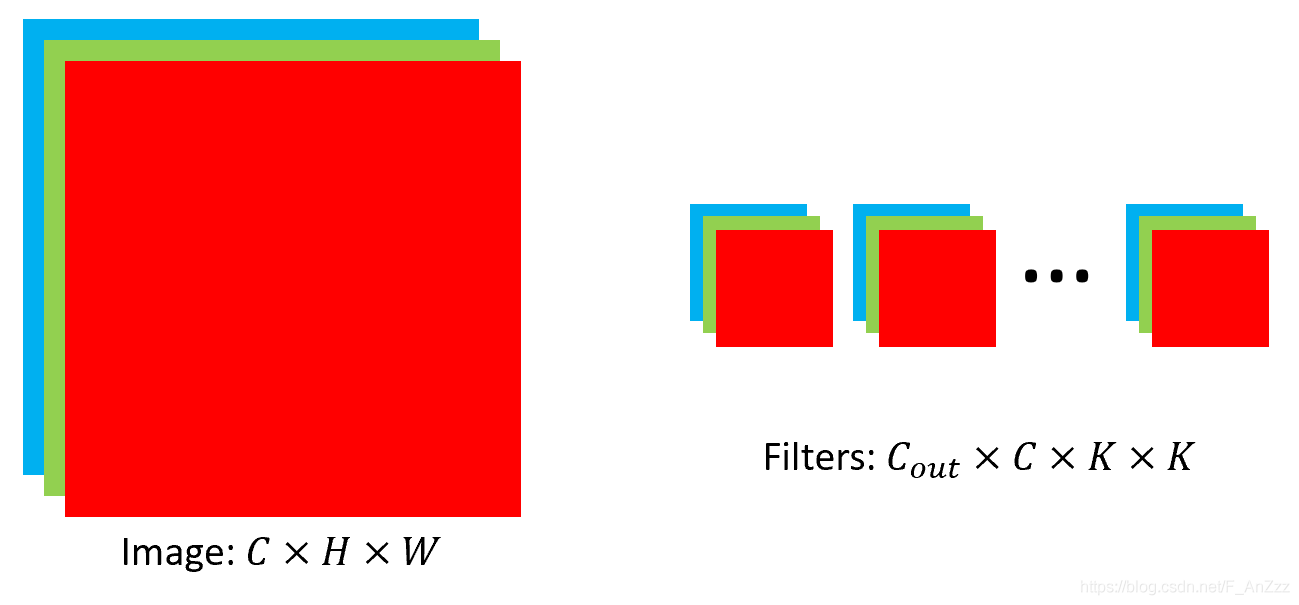
第一步：分别将特征图和卷积转换为矩阵

卷积核

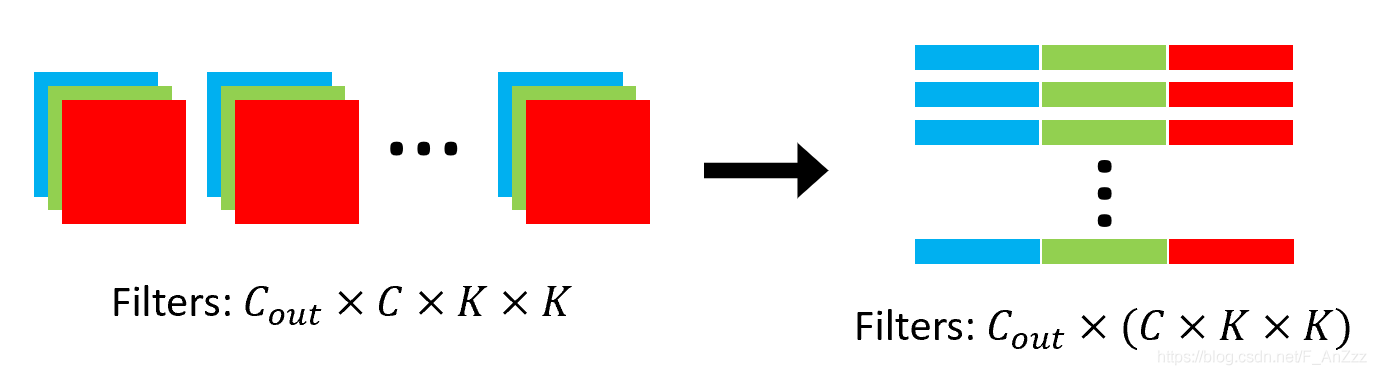
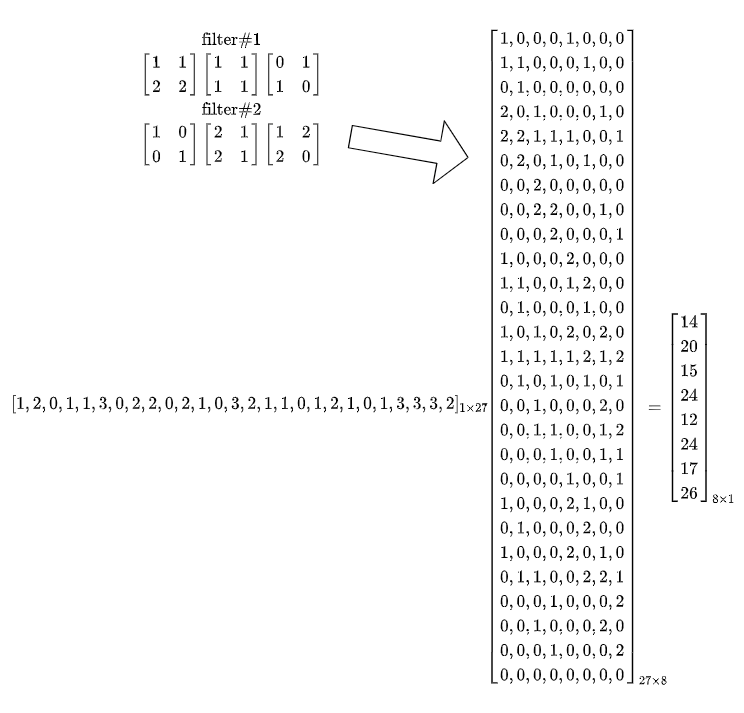
对于2D卷积，本身是四维的卷积核，将其转换为二维由$C_{\text {out }} \times C \times K \times K$变为$C_{\text {out }} \times M$，其中$M=C \times K \times K$。

例如，如下卷积核的维度是$2 \times 3 \times 2 \times 2$，分别为 filter 1 和 filter 2。

$$ \left[\begin{array}{ll} 1 & 1 \\ 2 & 2 \end{array}\right]\left[\begin{array}{ll} 1 & 1 \\ 1 & 1 \end{array}\right]\left[\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right] $$

$$ \left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]\left[\begin{array}{ll} 2 & 1 \\ 2 & 1 \end{array}\right]\left[\begin{array}{ll} 1 & 2 \\ 2 & 0 \end{array}\right] $$

转换成$C_{\text {out }} \times M$矩阵为$2 \times 12$大小，如下： $$ \left[\begin{array}{llllllllllll} 1 & 1 & 2 & 2 & 1 & 1 & 1 & 1 & 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 & 2 & 1 & 2 & 1 & 1 & 2 & 2 & 0 \end{array}\right] $$

特征图

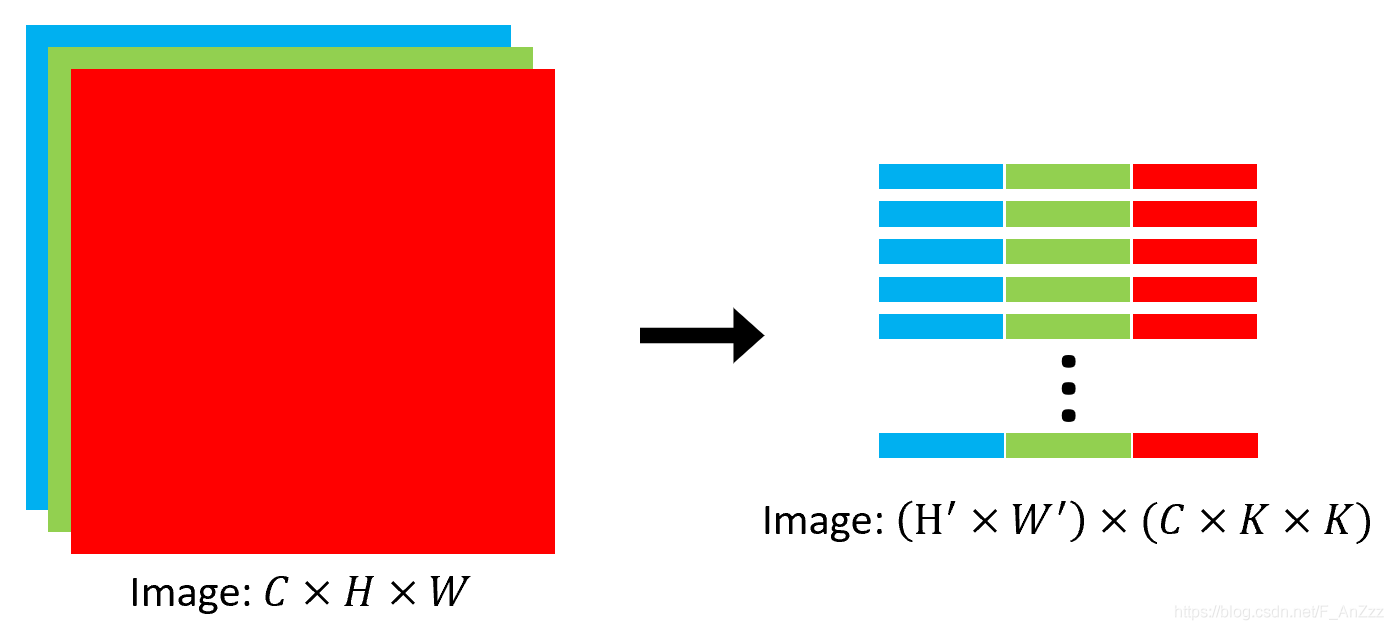
对于输入为$C \times H \times W$的特征图, 将其转换为$\left(H^{\prime} \times W^{\prime}\right) \times(C \times K \times K)$的矩阵。其中$H^{\prime}$和 $W^{\prime}$为输出特征图的长和宽。与卷积核kernel的变换不同，feature map不是单纯将矩阵resize一下就行, 而是要根据卷积核的尺寸、与特征图的作用过程需要的stride和padding，从输入特征中选择相应的值组成转换后的矩阵。

例如, 假设输入的特征图的大小为 $3 \times 3 \times 3$, 特征图为： $$ \left[\begin{array}{lll} 1 & 2 & 0 \ 1 & 1 & 3 \ 0 & 2 & 2 \end{array}\right]\left[\begin{array}{lll} 0 & 2 & 1 \ 0 & 3 & 2 \ 1 & 1 & 0 \end{array}\right]\left[\begin{array}{lll} 1 & 2 & 1 \ 0 & 1 & 3 \ 3 & 3 & 2 \end{array}\right] $$ 采用 $2 \times 2$ 卷积核, stride为 $1$, padding为 $0$ ，转换得到如下： $$ \left[\begin{array}{llllllllllll} 1 & 2 & 1 & 1 & 0 & 2 & 0 & 3 & 1 & 2 & 0 & 1 \ 2 & 0 & 1 & 3 & 2 & 1 & 3 & 2 & 2 & 1 & 1 & 3 \ 1 & 1 & 0 & 2 & 0 & 3 & 1 & 1 & 0 & 1 & 3 & 3 \ 1 & 3 & 2 & 2 & 3 & 2 & 1 & 0 & 1 & 3 & 3 & 2 \end{array}\right] $$ 这样, 最终的计算结果就变成了
$F \times C^{T}=\left(\left(H^{\prime} \times W^{\prime}\right) \times(C \times K \times K)\right) \times\left(C_{\text {out }} \times(C \times K \times K)\right)^{T}=\left(H^{\prime} \times W^{\prime}\right) \times C_{\text {out }}$
整体的流程可以简化为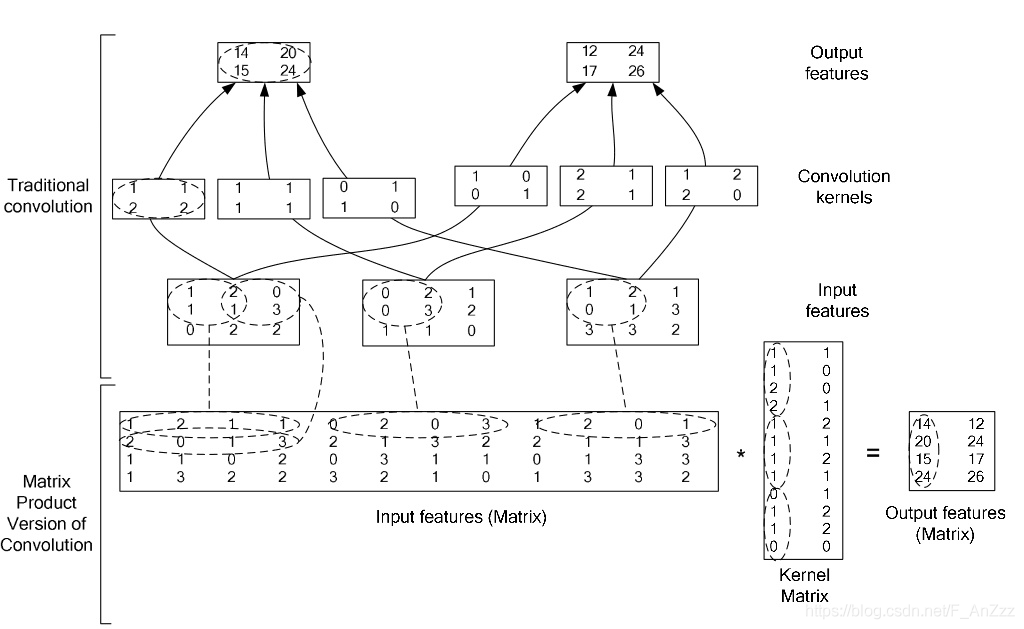下面用代码实现上面卷积过程：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


import torch 
from torch.nn.functional import unfold, fold

x = torch.Tensor([[[[1, 2, 0], [1, 1, 3], [0, 2, 2]], [[0, 2, 1], [0, 3, 2], [1, 1, 0]], [[1, 2, 1], [0, 1, 3],[3, 3, 2]]]])
print(x.shape)
weight = torch.Tensor([[[[1, 1], [2, 2]], [[1, 1], [1, 1]], [[0, 1], [1, 0]]], [[[1, 0], [0, 1]], [[2, 1], [2, 1]], [[1, 2], [2, 0]]]])
print(weight.shape)
kernel_size = 2
F = unfold(x, kernel_size).transpose(1, 2)
print(F)
C = weight.view(weight.size(0), -1)
print(C)
# F x C'
out_unf = F.matmul(C.t())
print(out_unf)
out = fold(out_unf.transpose(1, 2), (2, 2), (1, 1))
print(out)
print(out.shape)

如果把特征图按照行优先展开为一维向量，那么对应的卷积操作如下：

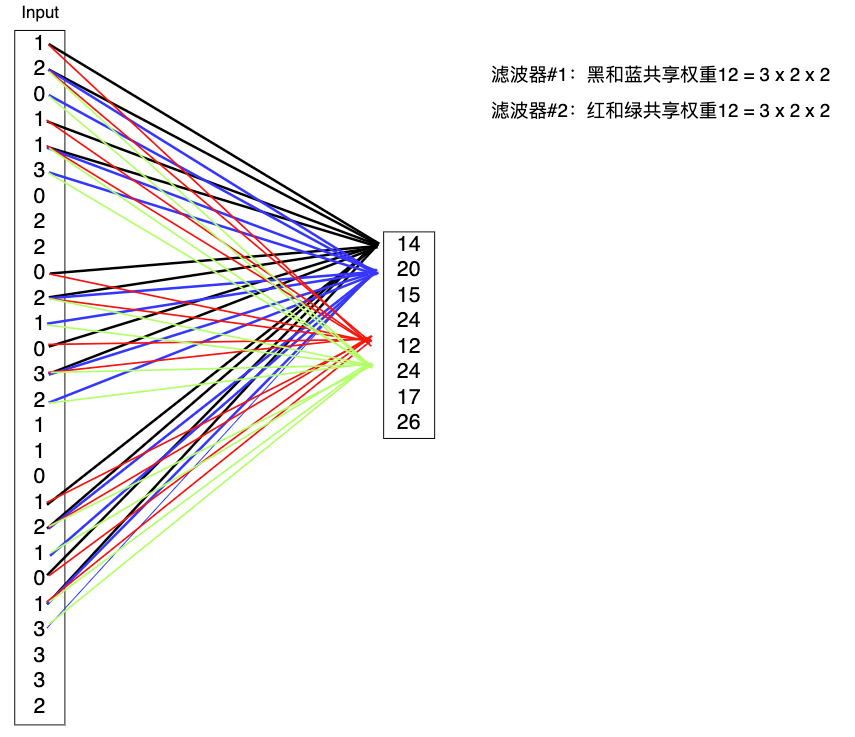
总结与分析

输出层的节点值并不是由全部输入层的节点值与权重乘积和得到，而只有部分输入节点参与到计算；从另一的角度可以当成是有一部分权重为零。
有大量权重被共享，有几个滤波器就共享了几套权重参数，这点原因应该是空间平移不变性，即某一区域和另一区域并没有差别。
上面将所有特征图拉成一维向量，这样只是和全连接层做对比，实际上，因为图像数据存在多通道，例如一般情况下的RGB三通道图像，每个通道包含一个维度的信息；另外图像中像素点之间的位置信息在二维图像中可以更好的呈现（编码），而拉成一维向量会丢失这些信息。
从信息论角度来说，三通道图像是否有图形的信息存在冗余。

参考：

卷积计算的底层实现
 YJango的卷积神经网络

更新记录

调整格式和排版。 —— 2022.07.19